Trinomio Cuadrado Perfecto

Se llama trinomio cuadrado perfecto al trinomio (polinomio de tres términos) tal que, dos de sus términos son cuadrados perfectos y el otro término es el doble producto de las bases de esos cuadrados. Se eleva al cuadrado El signo se define en el segundo termino.

Se llama trinomio cuadrado perfecto al trinomio (polinomio de tres términos) tal que, dos de sus términos son cuadrados perfectos y el otro término es el doble producto de las bases de esos cuadrados.

En el trinomio cuadrado perfecto los términos cuadrados son siempre positivos, en cambio el término del doble producto puede ser negativo; en este caso debe ser negativo uno de los términos del binomio cuyo cuadrado es el trinomio dado, del ejemplo anterior tenemos:

Ambas son respuestas aceptables.

Regla para conocer si un trinomio es cuadrado perfecto.

Un trinomio ordenado con relación a una letra es cuadrado perfecto cuando la primera y tercer letra son cuadrados perfectos (o tienen raíz cuadrada exacta) y son positivos y el segundo termino es el doble producto de sus raíces cuadradas.

Ejemplos:

Video de Ayuda

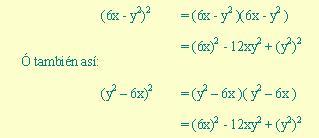
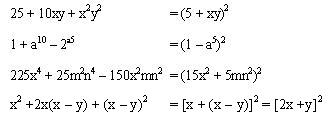
Comentarios

Entradas populares de este blog

Caso 1: Factor Común

Caso 1 Factor Común Un factor común monomio, es el factor que está presente en cada término del polinomio. En el caso de los coeficientes numéricos el factor común es el mayor divisor posible entre ellos y el factor común literal está conformado por el o los elementos de la parte literal presentes en todos los términos con el menor exponente. Para factorizar el polinomio, se escribe el factor común monomio multiplicado por el polinomio resultante de dividir cada término del polinomio original entre el factor común monomio. Ejemplos Factorizar El factor común numérico es el 6, puesto que 6 es el mayor divisor entre 12, 18 y 24 (nótese que 3 es divisor de 12, 18 y 24, pero el que necesitamos es el mayor posible), luego no tenemos factor común literal ya que no hay elementos en cada factor literal que se repita en todos los términos, por lo tanto, la factorización es: 6 ( 2 x ) + 6 ( 3 y ) − 6 ( 4 z ) = 6 ( 2 x + 3 y − 4 z ) Video de ayuda

Caso 5: Diferencia de cuadrados

Caso 5 Diferencia de Cuadrados La diferencia de cuadrados es una práctica que necesitamos tener clara para seguir avanzando en nuestro curso de Álgebra . Lo primero de todo es entender el concepto, saber qué significa la diferencia de cuadrados y cómo podemos ponerla en práctica. Por lo tanto, empecemos por el principio, la definición de diferencia de cuadrados. Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta. Al estudiar los productos notables teníamos que: En donde el resultado es una diferencia de cuadrados, para este capítulo es el caso contrario: Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases . Pasos a seguir para calcula la diferencia de cuadrados: Se extrae la raíz cuadrada de ambos términos. Se multiplica la suma por la diferencia de estas cantidades (el segundo termino del binomio negativo es la raíz del termino del ...

Caso 2: Factorización por agrupamiento

Caso 2 Factorización por agrupamiento Descomponer ax + bx + ay + by Los dos primeros términos tienen el factor común x y los dos últimos el factor común y . Agrupamos los dos primeros en un paréntesis y los dos últimos en otro precedido del signo + porque el tercer término tiene el signo (+): ax + bx + ay + by = (ax + bx ) + (ay + by ) = x (a + b ) + y (a + b ) = (a + b )(x + y ) Hay varias formas de hacer la agrupación, con la condición de que los dos términos agrupados tengan algún factor común, y siempre que las cantidades que quedan dentro de los paréntesis después de sacar el factor común en cada grupo, sean exactamente iguales. Si esto no es posible, la expresión dada no se puede descomponer por este método. En el ejemplo anterior podemos agrupar el 1o. y 3er. términos con el factor común a y el 2o. y 4o. con el factor común b, y: ax + bx + ay + by = (ax + ay ) + (bx + by ) = a(x + y ) + b (x + y ) = (x + y )(a + b ) Vide...

Temas de Matemáticas

Buscar este blog